Logarithms are a key mathematical concept used across various disciplines, from algebra to engineering and computer science. They help simplify complex calculations, solve exponential equations, and understand the behavior of growth patterns in real-world scenarios. This article will provide an in-depth explanation of logarithms, logarithmic properties, and how to solve logarithmic equations.
What is a Logarithm?
A logarithm is the inverse operation of exponentiation. In simple terms, while exponentiation involves raising a number to a power, a logarithm helps you find what exponent was used to get that number. If we have an exponential equation:
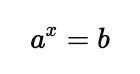
The logarithmic form of this equation is:
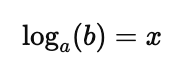
Where:
- $a$ is the base of the logarithm,
- $b$ is the argument of the logarithm (the result of raising $a$ to $x$),
- $x$ is the logarithm or exponent.
In words, $\log_a(b)$ is the exponent to which $a$ must be raised to produce $b$.
Common Logarithms
- Natural Logarithms: The logarithm with base $e$, written as $\ln(x)$, where $e \approx 2.71828$ is Euler’s number, commonly appears in growth and decay models.
- Common Logarithms: The logarithm with base 10, written as $\log(x)$, is often used in scientific calculations.
Properties of Logarithms
Logarithms follow several fundamental properties that make them useful in simplifying complex expressions. Understanding these properties is crucial when solving logarithmic equations.
1. The Product Rule
The logarithm of a product is the sum of the logarithms:
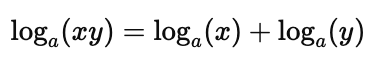
2. The Quotient Rule
The logarithm of a quotient is the difference of the logarithms:
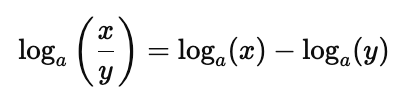
3. The Power Rule
The logarithm of a number raised to a power is the product of the exponent and the logarithm:
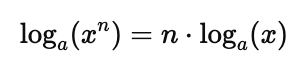
4. Change of Base Formula
If you need to change the base of a logarithm, you can use the following formula:
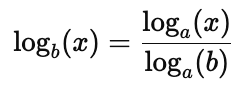
This is particularly useful when calculating logarithms on a calculator that only provides natural logarithms ($\ln$) and common logarithms ($\log$).
Solving Logarithmic Equations
Logarithmic equations are equations that involve logarithms of unknown variables. Solving them usually requires the use of logarithmic properties and converting between logarithmic and exponential forms. Here’s how to solve the most common types of logarithmic equations:
1. Basic Logarithmic Equation
Consider the equation:
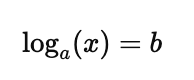
To solve for $x$, you can rewrite the equation in its exponential form:
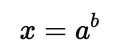
Example: Solve $\log_3(x) = 4$.
Convert to exponential form:
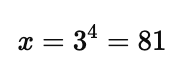
2. Logarithmic Equation with Multiple Logarithms
If the equation involves more than one logarithmic term, use the properties of logarithms to simplify and solve. For example:
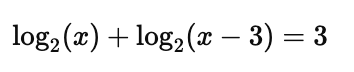
Step 1: Use the product rule:
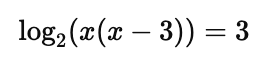
Step 2: Convert to exponential form:
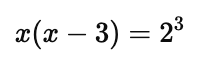
Step 3: Solve the quadratic equation:
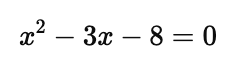
Use the quadratic formula:
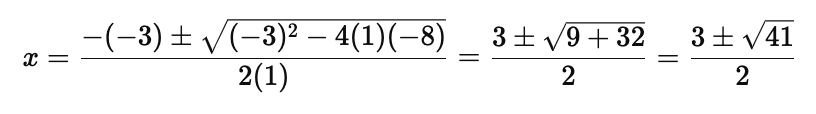
Thus, the solutions are:
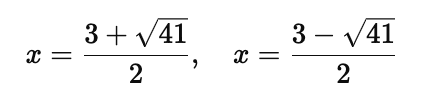
However, logarithms are only defined for positive arguments, so discard any negative solution if it makes the argument negative.
3. Equations with Logarithms on Both Sides
Sometimes you’ll have logarithmic terms on both sides of the equation. In this case, you can often solve by “canceling” the logarithms if the bases are the same.
Example: Solve $\log_5(x + 1) = \log_5(3x – 2)$.
Since the bases are the same, you can set the arguments equal to each other:
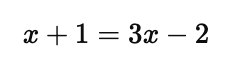
Solve for $x$:
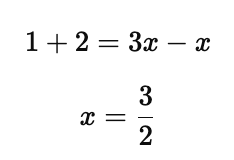
Applications of Logarithms
Logarithms have a wide range of applications in various fields. Here are a few prominent examples:
1. Exponential Growth and Decay
In fields like biology, physics, and economics, logarithms are used to model exponential growth (such as population growth) and exponential decay (like radioactive decay).
The general form of an exponential growth model is:
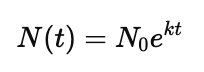
Where $N(t)$ is the quantity at time $t$, $N_0$ is the initial quantity, $k$ is the growth rate, and $t$ is time. Taking the natural logarithm on both sides allows you to solve for unknowns, such as the growth rate $k$.
2. Richter Scale (Earthquakes)
The Richter scale, which measures the magnitude of earthquakes, is logarithmic. A one-unit increase on the scale represents a tenfold increase in the earthquake’s amplitude. Thus, a magnitude 6 earthquake is 10 times more powerful than a magnitude 5 earthquake.
3. pH Scale (Acidity)
The pH scale measures the acidity of a solution and is logarithmic. It is defined as:
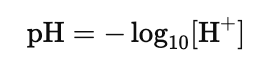
Where $[\text{H}^+]$ is the concentration of hydrogen ions. A difference of 1 pH unit corresponds to a tenfold change in acidity.
4. Entropy in Information Theory
In computer science and information theory, logarithms are used to measure information entropy, which quantifies uncertainty. The formula for entropy is:
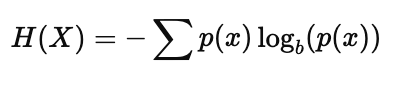
Where $H(X)$ is the entropy of a random variable $X$, and $p(x)$ is the probability of occurrence of each possible value.
Common Mistakes to Avoid
- Misapplying Logarithmic Rules: Ensure that you use the properties of logarithms correctly. For example, $\log_a(x + y) \neq \log_a(x) + \log_a(y)$, which is a common mistake.
- Ignoring the Domain: Logarithms are only defined for positive numbers. Always check that your solution does not make the argument of the logarithm negative or zero.
- Incorrect Exponential Conversion: When solving logarithmic equations, always double-check your conversion to the exponential form to ensure accuracy.
Conclusion
Logarithms are a powerful tool in mathematics, providing insight into exponential relationships and simplifying complex calculations. By understanding the core properties and how to solve logarithmic equations, you can tackle a wide range of problems, from algebraic expressions to real-world applications like measuring earthquakes or calculating growth rates. Mastery of logarithms opens the door to deeper mathematical understanding and problem-solving skills across numerous disciplines.

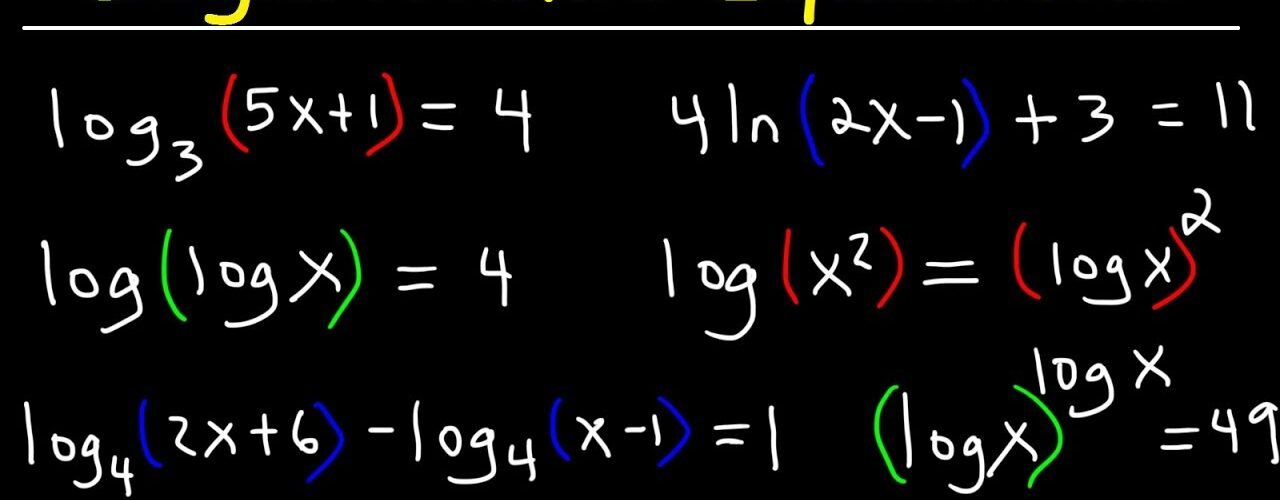

Add comment