Pythagorean Theorem

The Pythagorean Theorem is one of the most well-known and fundamental concepts in geometry, and its applications stretch far beyond the realm of mathematics. Named after the ancient Greek mathematician Pythagoras, this theorem serves as the foundation for solving problems involving right-angled triangles. In this article, we will dive into the Pythagorean Theorem, explore its proof, and discuss its wide-ranging applications.

What is the Pythagorean Theorem?

The Pythagorean Theorem applies to right-angled triangles, which are triangles where one of the angles measures exactly ${90}^{\circ }$. It provides a relationship between the lengths of the sides of the triangle:

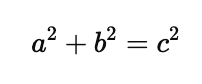
Where:

• $a$ and $b$ are the lengths of the legs (the two sides adjacent to the right angle),
• $c$ is the length of the hypotenuse (the side opposite the right angle).

In words, the Pythagorean Theorem states that the square of the hypotenuse is equal to the sum of the squares of the two legs.

Example of Using the Pythagorean Theorem

Consider a right-angled triangle where the lengths of the two legs are $a=3$ and $b=4$. Using the Pythagorean Theorem, we can calculate the length of the hypotenuse $c$.

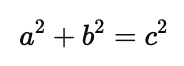
Substitute the values of $a$ and $b$:

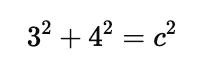
Simplify:

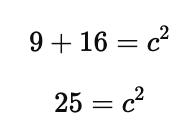
Taking the square root of both sides:

Thus, the hypotenuse is $5$ units long.

Proof of the Pythagorean Theorem

There are numerous proofs of the Pythagorean Theorem, ranging from geometric constructions to algebraic methods. Below is a simple geometric proof using area comparison.

Start with a square: Construct a large square with side length $(a+b)$, which contains a right-angled triangle with legs $a$ and $b$, and hypotenuse $c$.

Area of the large square: The area of the large square is $(a+b{)}^2$.

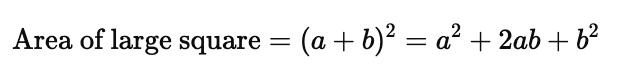
Triangles within the square: Now, place four identical right-angled triangles inside the square, each with legs $a$ and $b$ and hypotenuse $c$. The area of each triangle is $\frac{1}{2}ab$, and the total area of the four triangles is:

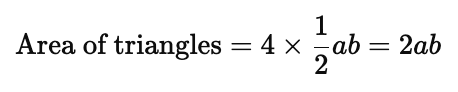
Remaining area (inner square): The space left inside the large square, not occupied by the triangles, forms a smaller square with side length $c$. The area of this inner square is $c^2$.

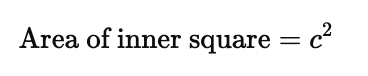
Equation for the large square: The area of the large square can also be expressed as the sum of the areas of the four triangles and the inner square:

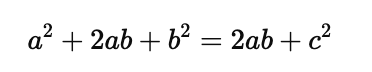
Simplify: Cancel $2ab$ from both sides:

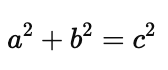
This completes the proof of the Pythagorean Theorem.

Applications of the Pythagorean Theorem

The Pythagorean Theorem has many practical applications across different fields, making it one of the most important tools in mathematics and science.

1. Distance Between Two Points

In coordinate geometry, the Pythagorean Theorem helps calculate the straight-line distance between two points on a plane. If you have two points $(x_1,y_1)$ and $(x_2,y_2)$, the distance between them is:

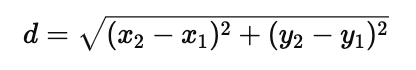
This formula is derived directly from the Pythagorean Theorem by considering the difference in $x$ and $y$ as the legs of a right triangle, with the distance $d$ as the hypotenuse.

2. Construction and Architecture

Builders and architects use the Pythagorean Theorem to ensure that structures are square and level. For example, if a carpenter is building a rectangular frame, they can measure the diagonals to check that they are equal. If the diagonals have the same length, the corners form right angles, ensuring the structure is properly aligned.

3. Computer Graphics and Game Development

In computer graphics, the Pythagorean Theorem helps calculate distances between pixels and determine how objects move or scale within a digital space. It’s essential for creating realistic movement, scaling, and collision detection in video games and animations.

4. Navigation and GPS Systems

The Pythagorean Theorem plays a crucial role in navigation, especially in determining the shortest path between two points. GPS systems use this principle to calculate distances and routes, simplifying travel directions for users.

Pythagorean Triples

A Pythagorean triple is a set of three positive integers $(a,b,c)$ that satisfy the Pythagorean Theorem. These triples are useful for constructing right-angled triangles with integer side lengths. The most famous Pythagorean triple is $(3,4,5)$, as shown in the earlier example.

Other common Pythagorean triples include:

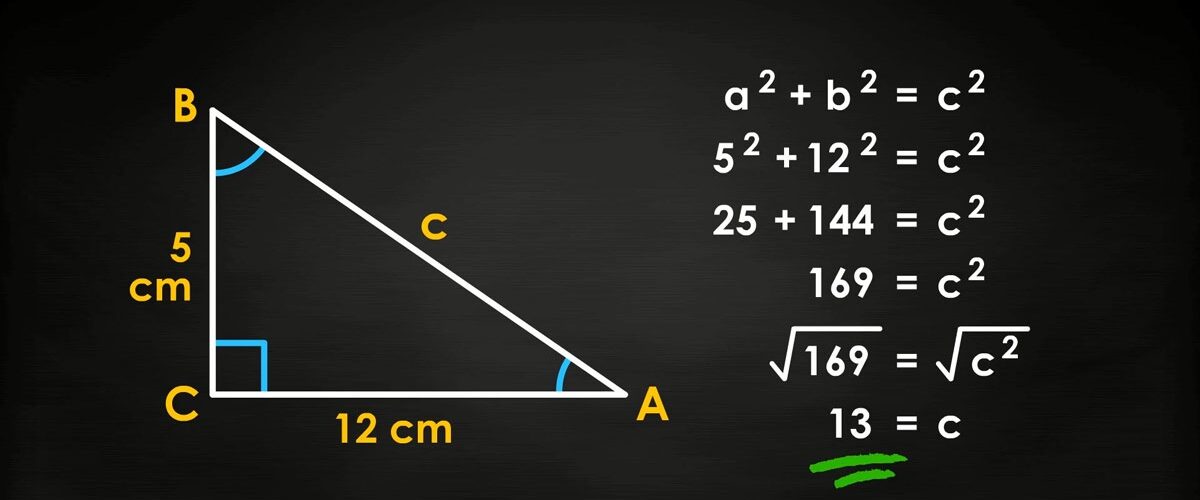
• $(5,12,13)$
• $(7,24,25)$
• $(8,15,17)$

These sets of numbers are useful in practical applications where exact measurements are needed.

Converse of the Pythagorean Theorem

The converse of the Pythagorean Theorem is also true: If the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, the triangle is a right-angled triangle. This property is often used in construction and engineering to verify whether a triangle is a right triangle.

For example, if you have a triangle with sides $a=6$, $b=8$, and $c=10$, you can check whether it’s a right triangle by verifying:

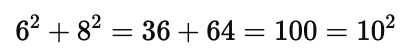
Since the equation holds true, the triangle is indeed a right triangle.

Common Mistakes to Avoid

1. Incorrect Identification of the Hypotenuse: The hypotenuse is always the side opposite the right angle, and it is the longest side of the triangle.
2. Forgetting to Square the Sides: A common mistake is forgetting to square the lengths of the legs and hypotenuse when applying the Pythagorean Theorem. Always remember that the formula involves the squares of the side lengths.
3. Misapplying the Theorem to Non-Right Triangles: The Pythagorean Theorem only applies to right-angled triangles. Ensure that you are working with a triangle that has a ${90}^{\circ }$ angle before using the theorem.

Conclusion

The Pythagorean Theorem is a powerful and versatile tool in mathematics, with applications ranging from geometry to engineering, navigation, and computer science. Its simplicity and elegance make it a cornerstone of mathematical reasoning. Whether you’re calculating distances, verifying the angles of a triangle, or solving real-world problems, the Pythagorean Theorem provides an essential framework for understanding the relationships between the sides of right-angled triangles.

By mastering this theorem and its applications, you’ll have a key mathematical tool at your disposal for solving a wide range of practical problems.