Heron’s Formula is a powerful and elegant method for calculating the area of a triangle when you know the lengths of all three sides. Named after the ancient Greek mathematician Heron of Alexandria, this formula offers a straightforward way to find the area without needing the height of the triangle. In this article, we will explain Heron’s Formula, provide a step-by-step guide on how to use it, and discuss its practical applications.
What is Heron’s Formula?
Heron’s Formula calculates the area of any triangle, provided you know the lengths of all three sides. Given a triangle with sides $a$, $b$, and $c$, the area of the triangle is given by:
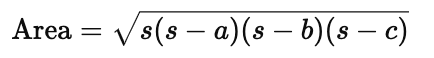
Where:
- $a$, $b$, and $c$ are the lengths of the triangle’s sides,
- $s$ is the semi-perimeter of the triangle, which is half of the perimeter. It is calculated as:
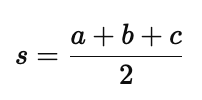
Step-by-Step Guide to Using Heron’s Formula
To use Heron’s Formula to find the area of a triangle, follow these simple steps:
Step 1: Find the Semi-Perimeter
First, calculate the semi-perimeter $s$ using the lengths of the sides $a$, $b$, and $c$. The formula for $s$ is:
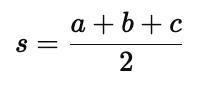
Step 2: Apply Heron’s Formula
Next, plug the values of $s$, $a$, $b$, and $c$ into Heron’s Formula:
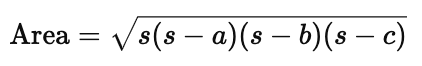
Step 3: Simplify and Solve
Finally, simplify the expression under the square root and calculate the area of the triangle.
Example of Using Heron’s Formula
Let’s use an example to demonstrate how Heron’s Formula works.
Consider a triangle with sides $a = 7$, $b = 8$, and $c = 9$. We will find the area of this triangle using Heron’s Formula.
Step 1: Calculate the Semi-Perimeter
First, calculate the semi-perimeter $s$:
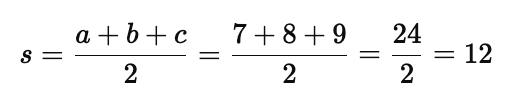
Step 2: Apply Heron’s Formula
Now, plug the values into Heron’s Formula:
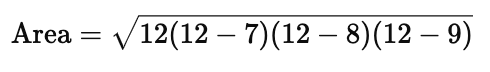
Simplify the terms inside the parentheses:
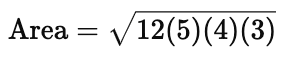
Multiply the values inside the square root:
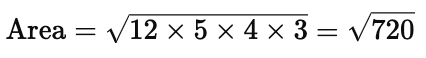
Step 3: Calculate the Area
Finally, take the square root of 720:
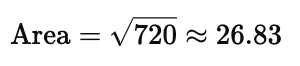
Thus, the area of the triangle is approximately $26.83$ square units.
When to Use Heron’s Formula
Heron’s Formula is particularly useful in the following situations:
- When you know all three sides of a triangle but not the height: Unlike the traditional formula for the area of a triangle ($\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$), Heron’s Formula doesn’t require knowledge of the height, making it a more versatile method for calculating the area of any triangle.
- For scalene triangles: In scalene triangles, where no two sides are equal and calculating the height can be difficult, Heron’s Formula provides a simple solution for finding the area.
- In geometry problems: Heron’s Formula is commonly used in various geometry and trigonometry problems, especially when solving for the area of irregular triangles.
Applications of Heron’s Formula
Heron’s Formula has practical applications in several fields, including:
1. Surveying and Land Measurement
In land surveying, Heron’s Formula is used to calculate the area of triangular plots of land, especially when the terrain is irregular, and it is difficult to measure heights.
2. Architecture and Construction
Architects and builders use Heron’s Formula to find the area of triangular sections in construction projects. It allows them to make precise calculations without needing to measure the height directly.
3. Physics and Engineering
In physics and engineering, Heron’s Formula is useful when dealing with triangular components of mechanical systems or triangular cross-sections in structures.
Proof of Heron’s Formula
Heron’s Formula can be derived using algebra and geometry, specifically by applying the law of cosines and trigonometric identities. Here’s an outline of the proof:
Start with the general formula for the area of a triangle using the sine of one of the angles. The area of a triangle can be written as:
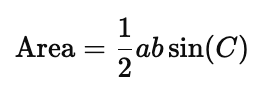
Where $C$ is the angle opposite side $c$.
Use the law of cosines to express $\cos(C)$ in terms of $a$, $b$, and $c$:
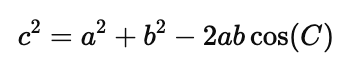
Solve for $\cos(C)$:
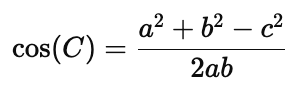
Apply a trigonometric identity to express $\sin(C)$ in terms of $\cos(C)$ and the sides of the triangle:
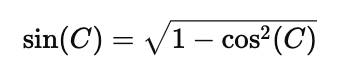
Substitute this into the formula for the area, and after some algebraic manipulation, you will eventually arrive at Heron’s Formula:
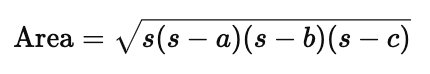
This is a condensed outline, but the full proof shows that Heron’s Formula is rooted in fundamental geometric and trigonometric principles.
Common Mistakes to Avoid
- Incorrect calculation of the semi-perimeter: Always remember to calculate the semi-perimeter correctly before applying the formula. Forgetting to divide the perimeter by 2 is a common mistake.
- Misapplying the formula to non-triangular shapes: Heron’s Formula only applies to triangles, so ensure that your problem involves a triangle before using the formula.
- Ignoring units: If your side lengths are given in specific units (such as meters or feet), make sure the area is expressed in square units (such as square meters or square feet).
Conclusion
Heron’s Formula is a powerful and versatile tool for calculating the area of any triangle, especially when the height is unknown. Its simplicity and general applicability make it a valuable formula in various fields, from land surveying and architecture to physics and engineering. By following the steps outlined in this article, you can easily use Heron’s Formula to solve problems involving triangles with known side lengths.
Whether you’re a student, a professional, or simply someone interested in geometry, mastering Heron’s Formula will give you a deeper understanding of the relationships between the sides and area of a triangle.

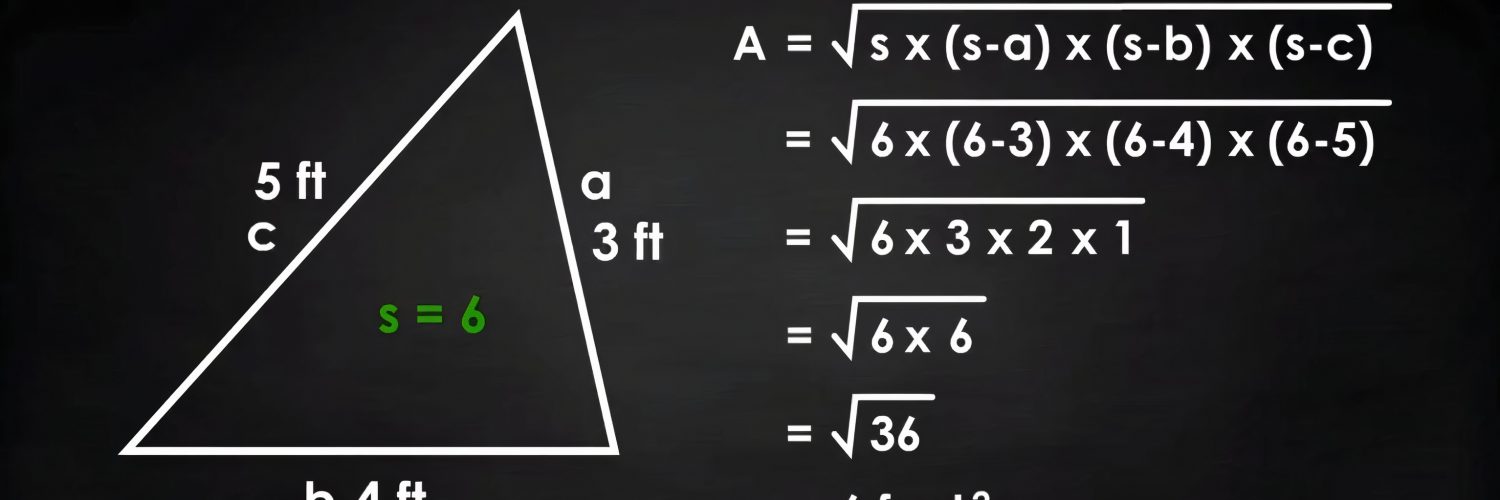

Let me know if you have any questions, I can answer all queries.
is it possible to do pythagoream theorem article??
Sure, I can make an article on the Pythagorean Theorem. If you tell me your email I can send the article to you when it is completed.