Derivatives are one of the most fundamental concepts in calculus, and they play a critical role in understanding how functions change. Whether you’re a student new to calculus or someone looking to refresh their knowledge, this guide will walk you through the core ideas of derivatives, their applications, and how to calculate them.
What Is a Derivative?
In simple terms, a derivative measures how a function changes as its input changes. Think of it as the rate of change or the slope of the curve at any given point. Mathematically, the derivative of a function $f(x)$ with respect to $x$ is denoted as $f'(x)$ or $\frac{d}{dx}f(x)$.
The Formal Definition of a Derivative
The formal definition of the derivative is rooted in limits. The derivative of a function $f(x)$ at a point $x = a$ is defined as:
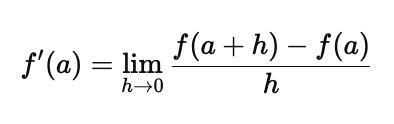
This expression is known as the difference quotient, and it gives us the slope of the tangent line to the curve at the point $x = a$. If this limit exists, we say the function is differentiable at that point.
Geometric Interpretation of Derivatives
The geometric interpretation of a derivative is crucial to understanding the concept. Imagine a curve plotted on the coordinate plane. At any specific point on the curve, the derivative tells you the slope of the tangent line at that point. The steeper the slope, the larger the derivative’s value.
- A positive derivative means the function is increasing at that point (slopes upward).
- A negative derivative means the function is decreasing (slopes downward).
- A zero derivative indicates that the function has a horizontal tangent line, which could be a maximum, minimum, or an inflection point.
Notations for Derivatives
There are several ways to notate a derivative:
- Leibniz Notation: $\frac{dy}{dx}$, where $y = f(x)$. This notation emphasizes the relationship between two variables.
- Lagrange Notation: $f'(x)$, which is more compact and commonly used.
- Newton’s Notation: $\dot{y}$, used primarily in physics, denotes the time derivative of a function $y$.
Rules of Differentiation
To compute derivatives efficiently, calculus provides several rules. Here are the most important ones:
1. The Power Rule
The power rule is one of the simplest and most frequently used rules in differentiation. If $f(x) = x^n$, where $n$ is any real number, then the derivative is:
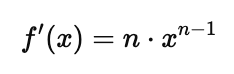
Example: If $f(x) = x^5$, then $f'(x) = 5x^4$.
2. The Product Rule
If you have a product of two functions, say $f(x)$ and $g(x)$, the derivative of the product is:
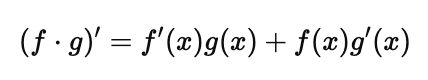
Example: If $f(x) = x^2$ and $g(x) = e^x$, then:
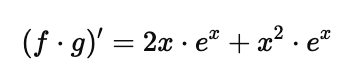
3. The Quotient Rule
The quotient rule helps differentiate functions in the form $\frac{f(x)}{g(x)}$:
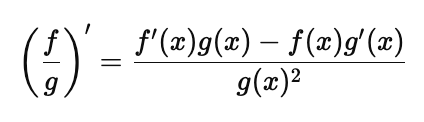
Example: If $f(x) = x^2$ and $g(x) = \sin(x)$, then:
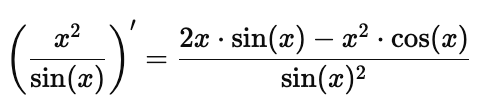
4. The Chain Rule
The chain rule is used when differentiating a composition of functions. If $y = f(g(x))$, the derivative is:
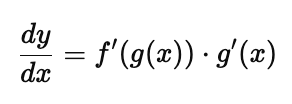
Example: If $f(x) = \sin(x^2)$, then:
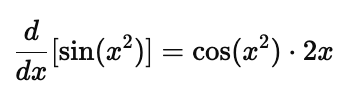
Higher-Order Derivatives
The derivative of a derivative is called a second derivative, and we denote it as $f”(x)$ or $\frac{d^2}{dx^2} f(x)$. Higher-order derivatives provide information about the curvature and concavity of the graph.
- If $f”(x) > 0$, the function is concave up.
- If $f”(x) < 0$, the function is concave down.
The second derivative is often used in physics to analyze acceleration, which is the rate of change of velocity.
Applications of Derivatives
Derivatives have a wide range of applications in various fields, from physics and engineering to economics and biology. Here are a few notable applications:
1. Optimizing Functions
One of the most common applications of derivatives is finding the maximum or minimum values of a function. This is critical in fields like economics, where you might want to maximize profit or minimize cost.
- To find the critical points of a function $f(x)$, solve $f'(x) = 0$.
- To determine whether a critical point is a maximum or minimum, use the second derivative test:
- If $f”(x) > 0$, it’s a local minimum.
- If $f”(x) < 0$, it’s a local maximum.
2. Motion and Physics
In physics, derivatives are used to describe the motion of objects. The velocity of an object is the derivative of its position function, and acceleration is the derivative of velocity.
If $s(t)$ represents the position of an object at time $t$, then:
- $v(t) = \frac{ds}{dt}$ is the velocity,
- $a(t) = \frac{dv}{dt} = \frac{d^2s}{dt^2}$ is the acceleration.
3. Economics: Marginal Analysis
In economics, derivatives help determine marginal cost, marginal revenue, and marginal profit. These concepts are essential for decision-making processes like determining the level of output that maximizes profit.
- The marginal cost is the derivative of the total cost function.
- The marginal revenue is the derivative of the total revenue function.
By setting marginal cost equal to marginal revenue, firms can determine the profit-maximizing level of output.
Differentiability and Continuity
It’s important to note that if a function is differentiable at a point, it must also be continuous at that point. However, the converse is not necessarily true: a function can be continuous at a point but not differentiable there (for example, at sharp corners or cusps in the graph).
Conclusion
Derivatives form the cornerstone of calculus, providing powerful tools to analyze change. From the rate of motion in physics to optimizing functions in economics, the derivative offers a window into understanding how variables interact and evolve. Mastering the rules of differentiation and understanding its real-world applications allows you to solve complex problems in both theoretical and applied settings.
Whether you’re just beginning your journey in calculus or seeking to strengthen your grasp of the subject, derivatives are a vital concept that continues to shape the way we model and solve dynamic problems.

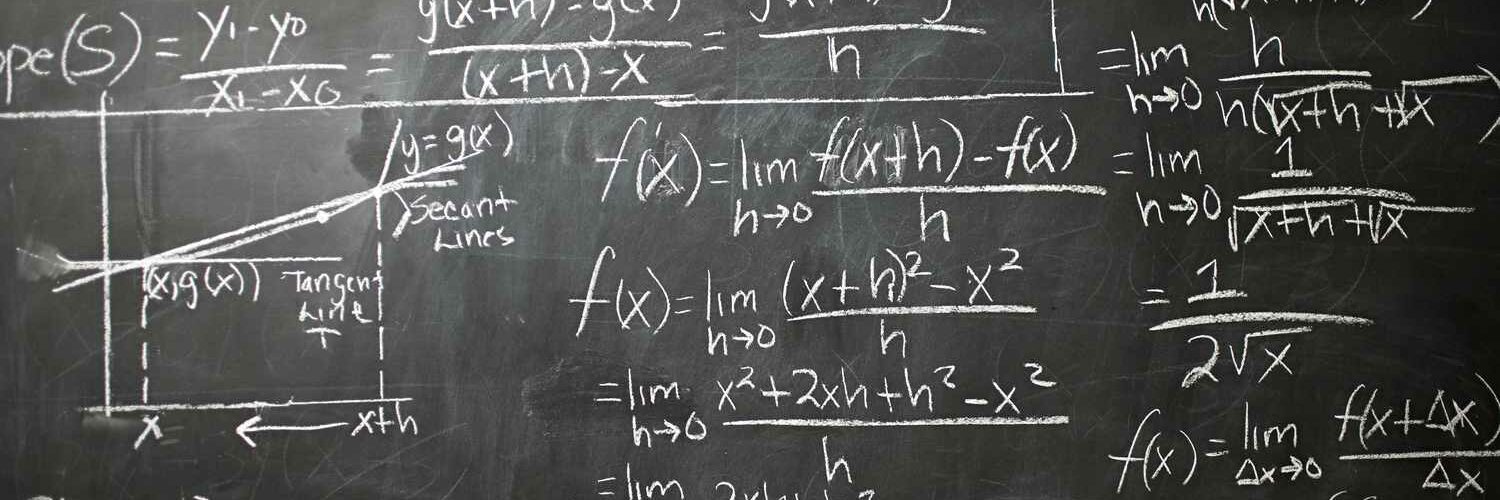
Add comment